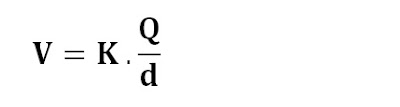Quando um corpo ou partícula com carga elétrica Q está em algum lugar do espaço, além do campo elétrico (campo vetorial), que já estudamos, produz também um campo escalar que associa a cada ponto ao seu redor um valor V chamado de potencial elétrico.
Também podemos criar uma "imagem mental" do potencial elétrico como sendo uma região sob influência da carga Q, mas que é traduzida por apenas um número para cada ponto, e não um vetor, como o campo elétrico.
Quando a carga elétrica Q for positiva, os pontos ao seu redor tem potencial positivo (um número positivo). Quando Q for negativa, os pontos têm potencial negativo (um número negativo).
Também podemos criar uma "imagem mental" do potencial elétrico como sendo uma região sob influência da carga Q, mas que é traduzida por apenas um número para cada ponto, e não um vetor, como o campo elétrico.
Quando a carga elétrica Q for positiva, os pontos ao seu redor tem potencial positivo (um número positivo). Quando Q for negativa, os pontos têm potencial negativo (um número negativo).
O potencial elétrico V em determinado ponto P depende apenas do valor de Q, e da distância d que separa P de Q, e é dado por:
Onde K é a constante eletrostática do meio onde a carga elétrica se encontra. É a mesma que vimos na Lei de Coulomb e para o campo elétrico. Para o vácuo, K=9 . 109Nm2/C2.
Onde K é a constante eletrostática do meio onde a carga elétrica se encontra. É a mesma que vimos na Lei de Coulomb e para o campo elétrico. Para o vácuo, K=9 . 109Nm2/C2.
Todos os pontos sob uma esfera imaginária de raio r, onde Q esteja no centro, possuem o mesmo potencial elétrico V; assim, essas superfícies são chamadas de equipotenciais, ou seja, tem o mesmo potencial elétrico.
A figura mostra duas esferas (imaginárias) concêntricas, 1 e 2, de raios r1 e r2, respectivamente. O potencial de qualquer ponto sobre a esfera 1 é V1, e de qualquer ponto sobre a esfera 2 é V2.
As superfícies dessas esferas são chamadas de equipotenciais.
A Unidade de Potencial Elétrico
A unidade de potencial elétrico no S.I é o volt (V), que corresponde ao Nm/C. Essa unidade é uma homenagem ao cientista italiano Alessandro Volta (1745 - 1827).
Em 1799, Volta criou a pilha elétrica, empilhando discos de 2 metais diferentes (cobre e zinco), separados por tecido umedecido com solução condutora. Daí o nome "pilha", como são chamadas atualmente algumas baterias. A partir delas, a eletricidade começou a nortear as atividades humanas, tanto em relação ao desenvolvimento das ciências, como do desenvolvimento de novas tecnologias.
O potencial elétrico V diminui proporcionalmente ao inverso da distância d que separa o ponto P da carga Q. Diferentemente do módulo do campo elétrico E, que diminui proporcionalmente ao inverso do quadrado daquela distância (d²). O potencial elétrico diminui mais "lentamente" em função do inverso apenas da distância d.
Imagine uma carga elétrica Q =5,0μC , e um ponto P distante d.
A figura mostra duas esferas (imaginárias) concêntricas, 1 e 2, de raios r1 e r2, respectivamente. O potencial de qualquer ponto sobre a esfera 1 é V1, e de qualquer ponto sobre a esfera 2 é V2.
As superfícies dessas esferas são chamadas de equipotenciais.
A Unidade de Potencial Elétrico
A unidade de potencial elétrico no S.I é o volt (V), que corresponde ao Nm/C. Essa unidade é uma homenagem ao cientista italiano Alessandro Volta (1745 - 1827).
Alessandro Volta (1745 - 1827)
Em 1799, Volta criou a pilha elétrica, empilhando discos de 2 metais diferentes (cobre e zinco), separados por tecido umedecido com solução condutora. Daí o nome "pilha", como são chamadas atualmente algumas baterias. A partir delas, a eletricidade começou a nortear as atividades humanas, tanto em relação ao desenvolvimento das ciências, como do desenvolvimento de novas tecnologias.
Pilha de Volta - 1799
O potencial elétrico V diminui proporcionalmente ao inverso da distância d que separa o ponto P da carga Q. Diferentemente do módulo do campo elétrico E, que diminui proporcionalmente ao inverso do quadrado daquela distância (d²). O potencial elétrico diminui mais "lentamente" em função do inverso apenas da distância d.
Imagine uma carga elétrica Q =5,0μC , e um ponto P distante d.
O potencial elétrico em P é dado, por:
Assim:
O interessante do potencial elétrico é que se existirem mais de uma carga elétrica na região, Q1, Q2 e Q3, por exemplo, o potencial elétrico VP em certo ponto P é dado pela simples soma desses potenciais.
Obs.: Vocês podem encontrar também o potencial elétrico sendo representado pela letra U, ok?
Questão
Três partículas com cargas elétricas QA= 5,0μC, QB = -10μC e QC = 2,0μC estão fixas numa região do espaço. Qual o potencial elétrico UP no ponto P devido à presença dessas partículas?
Resolução
Vamos determinar o potencial elétrico em P produzido por cada partícula:
Partícula A:
Partícula B:
Partícula C:
Então, o potencial UP em P, é:
Caso tivéssemos que calcular o campo elétrico E em P, obteríamos 3 vetores em direções diferentes, cuja soma vetorial nos daria muito trabalho para realizar. Conhecer o potencial elétrico pode nos ajudar a resolver de modo mais fácil alguns problemas que envolvem eletricidade.
Vamos avaliar o que aprendemos?
→ Clique aqui para testar o que aprendeu.
Questão
Três partículas com cargas elétricas QA= 5,0μC, QB = -10μC e QC = 2,0μC estão fixas numa região do espaço. Qual o potencial elétrico UP no ponto P devido à presença dessas partículas?
Resolução
Vamos determinar o potencial elétrico em P produzido por cada partícula:
Partícula A:
Partícula C:
Caso tivéssemos que calcular o campo elétrico E em P, obteríamos 3 vetores em direções diferentes, cuja soma vetorial nos daria muito trabalho para realizar. Conhecer o potencial elétrico pode nos ajudar a resolver de modo mais fácil alguns problemas que envolvem eletricidade.
Vamos avaliar o que aprendemos?
→ Clique aqui para testar o que aprendeu.